Posted by Random at 11:23am Aug 3 '05In 1859 Bernhard Tiemann, a little known thirty-two-year-old mathematician, made an incidental remark while presentaing a paper titled "On the Number of Prime Numbers Less Than a Given Quantity" to the Berlin Academy. He tossed out a guess, a hypothesis, which has proven to be almost cruelly compelling to countless scholares ever since. Today, after 150 years of careful research and exhaustive study, the question remains. Is the hypothesis true or false?
Riemann investigated straightforward arithmetic. To understand the issue, ask: How many prime numbers are there less than 20? The answer is eight: 2, 3, 5, 7, 11, 13, 17, and 19. How many are there less than one thousand? Less than one million? Less than one billion? Is the a general rule or formula for how many that will spare us the trouble of counting them?
Unlike other theorems, the Riemann Hypothesis is not easy to state in terms a nonmathematician can easily grasp. It lies deep in the heart of some quite abstruse mathematical theory. Here it is:
The Riemann zeta function is of central importance in the study of prime numbers. In its first form introduced by Euler, it is a function of a real variable x:
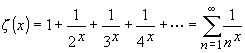
This series converges for every x > 1 (for x=1 it is the non-corvergent harmonic series).
Euler showed that this function can also be expressed as an infinite product which involves all prime numbers pn, n=1,...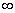
Riemann studied this function extensively and extended its definition to take complex arguments z. So the function
bears his name. Of particular interest are the roots of :
Riemann conjectured that all nontrivial zeros are at Re(z)=1/2. Although this has been shown to be true for more than the first billion nontrivial zeros, the conjecture remains open. A proof would establish new results in number theory, for example on the distribution of primes. The fact that Riemann Hypothesis holds for billions of nontrivial zeros does not guarantee anything. As noted by I. Good and R. Churchhouse in 1968, in the theories of zeta function and of primes distribution, one frequently meets terms like log log x, a function which increases extremely slow. The first nontrivial root not on Re(1/2) might have an imaginary part y such that log log y is of the order say 10. Then y would be 1010,000, a definitely unreachable number, computationally.
For a visual, we can direction plot the complex numbers resulting from ö(ý + òi) for ò from 0 to 80. The path returns continuously to {0,0}. After 10, if the curve ever missed the origin, the Riemann Hypothesis would be false.
The Riemann hypothesis asserts that all interesting solutions of the equation:
lie on a certain vertical straight line. This has been checked for the first 1,500,000,000 solutions. A proof that it is true for every interesting solution would shed light on many of the mysteries surrounding the distribution of prime numbers.
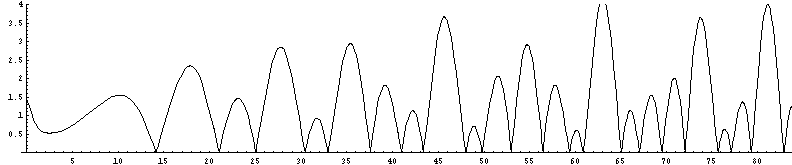
Mathematica can plot the Zeta function for complex values, so I plotted the absolute value of ö(1/2 + b I) and ö(1/3 + b I).
Whoever figures this one out is going to be pretty darn famous. So mainly, Reimann hypothesis: true or false?
Riemann investigated straightforward arithmetic. To understand the issue, ask: How many prime numbers are there less than 20? The answer is eight: 2, 3, 5, 7, 11, 13, 17, and 19. How many are there less than one thousand? Less than one million? Less than one billion? Is the a general rule or formula for how many that will spare us the trouble of counting them?
Unlike other theorems, the Riemann Hypothesis is not easy to state in terms a nonmathematician can easily grasp. It lies deep in the heart of some quite abstruse mathematical theory. Here it is:
The Riemann Hypothesis
All non-trivial zeros of the zeta function
have real part one-half.
All non-trivial zeros of the zeta function
have real part one-half.
The Riemann zeta function is of central importance in the study of prime numbers. In its first form introduced by Euler, it is a function of a real variable x:
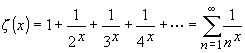
This series converges for every x > 1 (for x=1 it is the non-corvergent harmonic series).
Euler showed that this function can also be expressed as an infinite product which involves all prime numbers pn, n=1,...
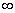
Riemann studied this function extensively and extended its definition to take complex arguments z. So the function
bears his name. Of particular interest are the roots of :
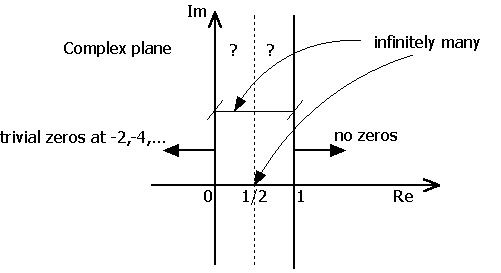
Trivial zeros are at z= -2, -4, -6, ...
Nontrivial zeros are at z such that 0 < Re(z)< 1 and there are infinite ones. Infinitely many lie in particular on
Re(z)=1/2 (proved in 1914 by the English number theorist Godfrey Hardy)
There are no zeros for Re(z)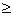
1. The case Re(z)=1 was proved in 1896 by Hadamard and de la Vallée-Poussin
and used in their proof of the Prime Number Theorem.
Riemann conjectured that all nontrivial zeros are at Re(z)=1/2. Although this has been shown to be true for more than the first billion nontrivial zeros, the conjecture remains open. A proof would establish new results in number theory, for example on the distribution of primes. The fact that Riemann Hypothesis holds for billions of nontrivial zeros does not guarantee anything. As noted by I. Good and R. Churchhouse in 1968, in the theories of zeta function and of primes distribution, one frequently meets terms like log log x, a function which increases extremely slow. The first nontrivial root not on Re(1/2) might have an imaginary part y such that log log y is of the order say 10. Then y would be 1010,000, a definitely unreachable number, computationally.
For a visual, we can direction plot the complex numbers resulting from ö(ý + òi) for ò from 0 to 80. The path returns continuously to {0,0}. After 10, if the curve ever missed the origin, the Riemann Hypothesis would be false.
The Riemann hypothesis asserts that all interesting solutions of the equation:
ö(s) = 0
lie on a certain vertical straight line. This has been checked for the first 1,500,000,000 solutions. A proof that it is true for every interesting solution would shed light on many of the mysteries surrounding the distribution of prime numbers.
Mathematica can plot the Zeta function for complex values, so I plotted the absolute value of ö(1/2 + b I) and ö(1/3 + b I).
|ö(1/2 + b I)| for b = 0 to 85. Note how often the function dips to zero.
|ö(1/3 + b I)| for b = 0 to 85. Note how often the function never dips to zero.
Whoever figures this one out is going to be pretty darn famous. So mainly, Reimann hypothesis: true or false?